What Is an Ellipse
If you don't know what is an ellipse you should imagine a wheel (e.g. bike wheel). It is blown off evenly.
Look at the picture!
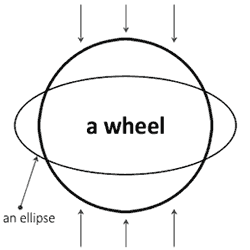
The wheel is unusable now but on the other hand we have a perfect ellipse. Our life helps us to know math!
So, what is an ellipse in math? An ellipse is a geometric figure. You can get it in the geometric plane.
Here is the canonical equation of the ellipse:
x2a2
+ y2b2
=1 ,Points:
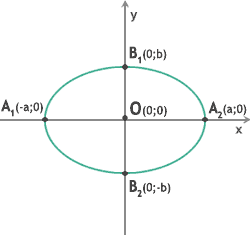
| O(0;0) | - | the centre of the ellipse |
| A1(-a;0) | - the tops of the ellipse | |
| A2(a;0) | ||
| B1(0;b) | ||
| B2(0;-b) | ||
| |A1A2| = 2a | - | the major axis of the ellipse |
| |B1B2| = 2b | - | the minor axis of the ellipse |
| |OA1| = |OA2| = a | - | the semimajor axis of the ellipse |
| |OB1| = |OB2| = b | - | the semiminor axis of the ellipse |
So, the canonical equation of the ellipse with the centre (0;0) and the semimajor axis a, the semiminor axis b is:
x2a2
+ y2b2
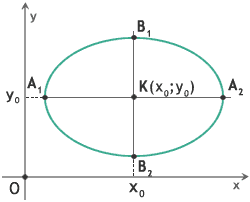
=1If you need an ellipse with the centre in the point K(xo;yo), then you should use the equation:
(x - xo)2a2
+ (y - yo)2b2
=1|KA1| = |KA2| = a - the semimajor axis of the ellipse
|KB1| = |KB2| = b - the semiminor axis of the ellipse
